Civil Engineering: Deflections Of Bents And Shear Walls

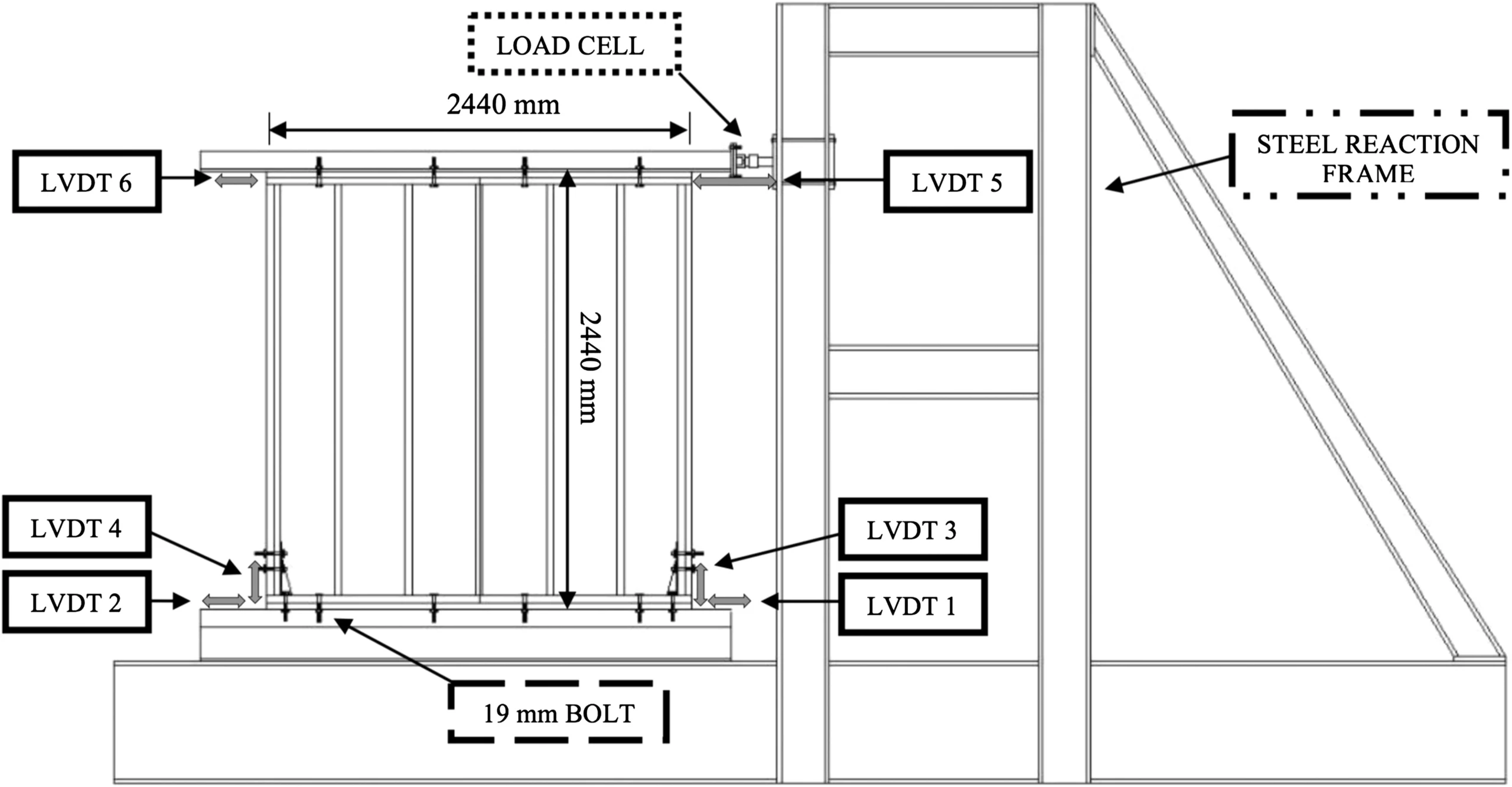
The horizontal deflections in the planes of bents and shear walls can be calculated doing a hypothesis that they act as cantilevers. Deflections of braced bents can be computed by the dummy-unit-load process or a matrix process. Deflections of rigid frames can be calculated by the addition of the drifts of the stories, as spotted by moment distribution or a matrix method.

Figure below showing Building frame defends lateral forces with (a) Wind bents (g) Shear walls or a combination of the two. Bents may be braced in any of several ways, including (b) X bracing, (c) K bracing, (d) inverted V bracing, (e) knee bracing, and (f) rigid connections.

For a shear wall (Fig) the deflection in its plane made by a load in its plane is the sum of the flexural deflection as a cantilever and the deflection due to shear. Thus, for a wall with solid rectangular cross section, the deflection at the top for uniform load is

Where …
w = uniform lateral load
H = height of the wall
E = modulus of elasticity of the wall material
t = wall thickness
L = length of wall
For a shear wall with a concentrated load P at the top, the deflection at the top is

Units used in these equations are those commonly functional in United States Customary System (USCS) and the System International (SI) measurements, that is, kip (kN), lb /in 2 (MPa), ft (m), and in (mm).

Where shear walls contain openings, such as those for doors, corridors, or windows, computations for deflection and inflexibility are more complexes. However approximate process can be obtained.

Source : Engineeringcivil.com